Глобальный интернет является всеобщим понятием и универсальным термином, характеризующим определенную стадию состояния и развития интернета, как составной части киберпространства.
Согласно концепции С. Дуна "Открытые веб-страницы", в применении к киберпространству является корректным и допустимым множество вариантов его представления (моделирования), а также способов и методов изучения.
В данной статье на основе множественной математической модели С. Дуна дается одно из определений Глобального Интернета и утверждается, что Глобальный Интернет является пределом последовательности элементов интернета. Для обозначения последовательности элементов интернета впервые применен термин открытый интернет.
1. Введение понятия открытый интернет для обозначения последовательности элементов множества Интернет.
Пусть задано множество Интернет I .
Тогда последовательностью элементов множества I называется отображение ƒ :  → I, такое что, каждому натуральному числу 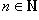 ставится в соответствие элемент xn, такой что xn ∈I (элемент xn множества I)
Последовательность (xn) назовем открытым интернетом и обозначим I
Предельное значение, или состояние, к которому стремится открытый интернет, назовем Глобальным Интернетом и обозначим IGL .
2. Теорема. Глобальный Интернет, как предельное значение открытого интернета, есть Бесконечность.
Открытый интернет I есть последовательность (xn), где
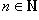
Очевидно,что последовательность (xn) является бесконечно большой, т.е.
lim xn = ∞
n → ∞
Пределом открытого интернета, как последовательности (xn), является бесконечность.
Глобальный Интернет также является пределом открытого интернета, т.е. пределом той же последовательности (xn).
На основании известной теоремы* последовательность не может иметь более одного предела.
Следовательно,
Глобальный Интернет есть бесконечность
lim xn = lim I = IGL = ∞
n → ∞ n → ∞
Значит, справедливо утверждение, что Глобальный Интернет, как предельное значение открытого интернета, есть Бесконечность.
*) рекомендуется найти соответствующую теорему в качестве упражнения
s.dun (с.дунец) © 2011
| 
Главная 
